
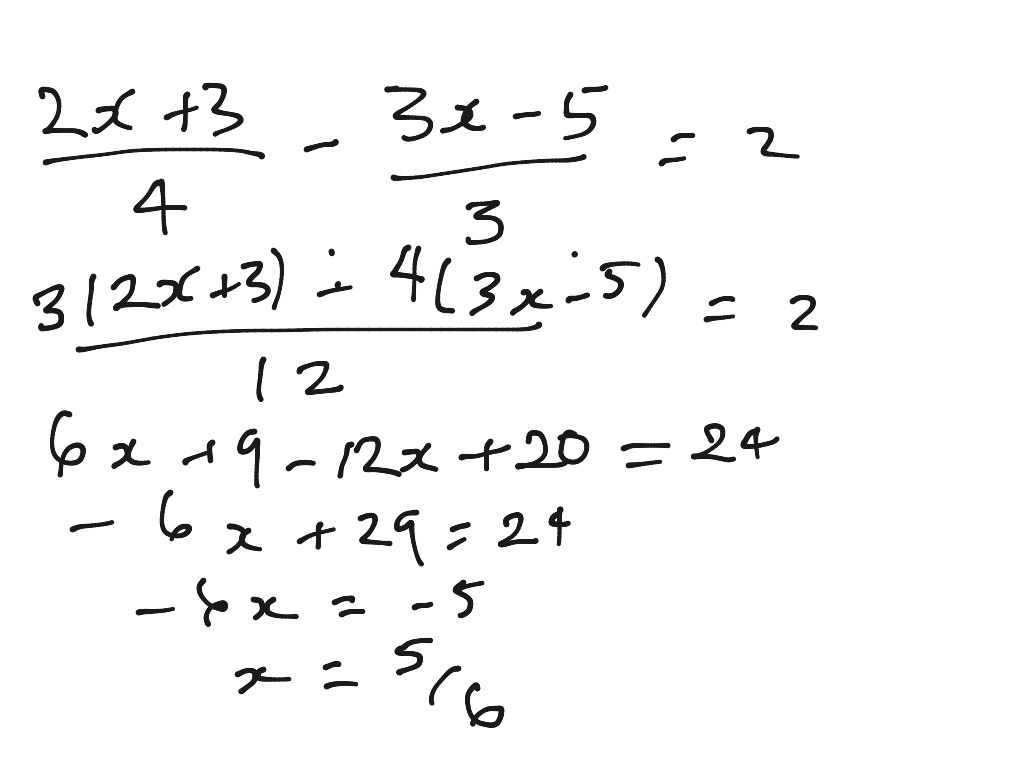
The remainder is therefore f(2) = 2×2³ - 3×2² - 3×2 + 2 = 0, as we saw when we divided the whole thing out. In the above example, 2x³ - 3x² - 3x + 2 was divided by x - 2. If a polynomial f(x) is divided by ax - b, the remainder is f(b/a) It is often useful to know what this remainder is and it can often be calculated without going through the process of dividing. When dividing one algebraic expression by another, more often than not there will be a remainder. This is easy to factorise, the answer being (x - 3)(x + 2). If you carry out the division, you will get x 2 - x - 6. Now we can divide x 3 -7x - 6 by (x + 1) to find the other factors. If you notice or have been told this, then you know immediately, by the factor theorem, that one of the factors is (x + 1). Note that if we replace x by -1, then we get zero. The factor theorem is important because it can be an easy way of finding factors that would otherwise be difficult to find.

This means that (x - 2) is a factor of the equation. In other words, if a polynomial f(x) can be divided by (x - a) without a remainder, then x = a is a root of f(x) (so f(a) = 0). If (x – a) is a factor of the polynomial f(x), then f(a) = 0
#How do you do division algebra equations how to#
With algebraic long division, practise makes perfect- the best way to learn how to do them properly is to do loads of examples until you get them right every time. For example, if you are dividing x³ + x - 4 by something, rewrite it as x³ + 0x² + x - 4. If the polynomial/ expression that you are dividing has a term in x missing, add such a term by placing a zero in front of it. The easiest way to explain it is to work through an example. If a = b, then a can be substituted for b in any expression.Algebraic long division is very similar to traditional long division (which you may have come across earlier in your education). This is called the substitution property of equality. Or in the numbers taken from the oak tree example It tells us that if a quantity a equals quantity b, and b equals the quantity, c, then a and c are equal as well. This property states that if quantity a equals quantity b, then b equals a.Īnother property that can be explained by this is the transitive property of equality. We can also use this example with the pieces of wood to explain the symmetric property of equality. This is called the reflexive property of equality and tells us that any quantity is equal to itself And then he continues on into making ten pieces that all are 6ft long before loading them onto his truck.īy looking at the different pieces of wood we can see that the following holds true. He first cuts it into two pieces that are both 30ft. He now wants to chop it into smaller pieces. George has cut down a 60ft high oak tree. There are a couple of other properties of equations that can be good to know as well Anything is acceptable as long as you do the same thing on both sides. This gives us a way to change an equation to our own liking. You can perform the same inverse operation on each side of an equivalent equation without changing the equality. addition and subtraction or multiplication and division. An inverse operation are two operations that undo each other e.g. And this as we learned in a previous section is shown by the equality sign =. Two equations that have the same solution are called equivalent equations e.g.


 0 kommentar(er)
0 kommentar(er)
